In contrast to other patch-based modeling approaches such as PCA, ICA or sparse coding, KPCA is capable of capturing nonlinear interactions of the basis elements of the image. The original form of KPCA, however, can be only applied to strongly restricted image classes due to the limited number of training examples that can be processed. We therefore propose a new iterative method for performing KPCA, the Kernel Hebbian Algorithm.

 

Kernel Principal Component Analysis

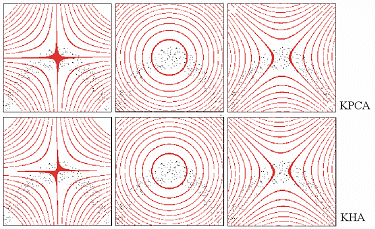
We investigate the analysis of images based on kernel PCA (KPCA). Memory and time complexity are, however, major obstacles for applying KPCA to huge image databases. The generalized Hebbian algorithm (GHA) provides an efficient implementation of linear PCA with smaller demands on memory complexity. Accordingly, we study the transfer of this property to KPCA by kernelizing the GHA.

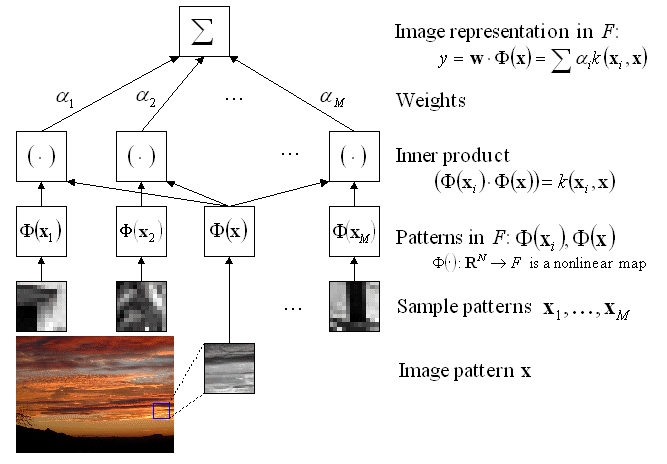
The basic idea of KPCA for image analysis is to nonlinearly map the data into a Reproducing Kernel Hilbert Space (RKHS) F and then perform linear PCA in F. The architecture of KPCA for the extraction of the first principal component is depicted in Fig. 1. A patch of a natural image is fed into the KPCA analyzer. A nonlinear map 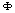is then applied to map the input into the RKHS F, where the inner product with the principal axis w is computed. These two operations are in practice performed in one single step using the kernel function 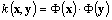. By expanding the solution w as a linear combination of mapped samples, KPCA indirectly performs PCA in F only based on the kernel function.

Kernel Hebbian Algorithm

In the original KPCA formulation, the combination coefficients are computed by diagonalizing the Gram matrix 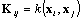for all sample patterns, which is prohibitive for natural images due to memory complexity. As a nonlinear extension of the  Hebbian algorithm, the Kernel Hebbian Algorithm (KHA) estimates them iteratively based on the correlation between the mapped patterns 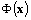and the system output y in F, which can be efficiently computed based on kernels. This relieves the burden of working directly in a possibly very high-dimensional RKHSs and storing the whole gram matrix.

Single-frame superresolution

Figs. 3 and 4 show applications of the KHA to image super-resolution. The problem is to reconstruct a high-resolution image based on a low-resolution image. It requires prior knowledge which in our case will be provided by the kernel principal components of a representative dataset of high-resolution image patches. To reconstruct a super-resolution image from a low-resolution image which was not contained in the training set, we first scale up the image to the same size as the training images, then map the image into the F, and project it into the KPCA subspace corresponding to a limited number of principal components. This reconstruction in F is projected back into the input space by preimage techniques.

Image denoising

Fig. 5 shows applications of the KHA to image denoising. No clean training images are required. Instead, it is assumed that the noise mainly contaminates the kernel principal components (KPCs) with small eigenvalues. Thus, a truncated KPC expansion of the noisy image leads automatically to a denoising effect. The KHA is trained and tested on the same data set.