image processing: research
Steganalysis
Steganography is the art of hidden storage or transmission of information. For instance, a message embedded in a harmlessly looking image can be used to communicate without attracting unwanted attention. The reverse process, the detection of the presence or absence of steganographic manipulation in an information-carrying medium is called steganalysis.
The goal of this project is the development of new and more powerful steganalysis methods for images, especially tools for the so-called universal steganalysis, i.e., steganalysis without knowing the specific method of steganographic manipulation. Universal steganalysis requires the statistical characterisation of unmanipulated images. In our case, we will build on our previous experience in image modeling (e.g., our kernel PCA or Wiener series image model) to describe the typical properties of unmanipulated images. A significant deviation from these properties in an image could be used to detect a steganographic manipulation.
Bats recognize the individual voices of other bats
Bats can use the characteristics of other bats' voices to recognize each other. This is one of the results of our recent collaborative study with Y. Yovel, M. Melcon, A. Denziger and H.-U- Schnitzler from the University of Tübingen. The study, published June 5 in the open-access journal PLoS Computational Biology, explains how bats use echolocation for more than just spatial knowledge.
We first tested the ability of four greater mouse-eared bats to distinguish between the echolocation calls of other bats. After observing that the bats learned to discriminate the voices of other bats, we developed a computer model based on machine learning techniques that reproduces the recognition behaviour of the bats. Analysis of our model suggests that the spectral energy distribution in the signals contains individual-specific information that allows one bat to recognize another.
Animals must recognize each other in order to engage in social behaviour. Vocal communication signals are helpful for recognizing individuals, especially in nocturnal organisms such as bats. Little is known about how bats perform strenuous social tasks, such as remaining in a group when flying at high speeds in darkness, or avoiding interference between echolocation calls. The finding that bats can recognize other bats within their own species based on their echolocation calls may therefore have some significant implications.
[ Link to the original paper, press echo in BBC Worlwide, ORF News, Discover Magazine. ]
In a previous study, we investigated whether machine learning algorithms can be used to extract biologically plausible features from complex ultrasound echoes created by ensonifying various plants with bat-like chirps. The resulting ultrasonic features turned out to be surprisingly simple: a few combinations of time-frequency channels were sufficient to classify plant echoes with high accuracy.
[ Link to the original paper, press echo in Science Now, Spiegel Online and Innovationsreport. ]
The reasons why plant classification is possible at all were investigated in a third study where we examined the statistics of natural vegetation echoes. Vegetation echoes constitute a major part of the sensory world of more than 800 species of echolocating bats and play an important role in several of their daily tasks. Our statistical analysis is based on a large collection of plant echoes acquired by a biomimetic sonar system. We explore the relation between the physical world (the structure of the plant) and the characteristics of its echo. Finally, we complete the story by analyzing the effect of the sensory processing of both the echolocation and the auditory systems on the echoes and interpret them in the light of information maximization. The echoes of all different plant species we examined share a surprisingly robust pattern that was also reproduced by a simple Poisson model of the spatial reflector arrangement. The fine differences observed between the echoes of different plant species can be explained by the spatial characteristics of the plants. The bat's emitted signal enhances the most informative spatial frequency range where the species-specific information is large. The auditory system filtering affects the echoes in a similar way, thus enhancing the most informative spatial frequency range even more. These findings suggest how the bat's sensory system could have evolved to deal with complex natural echoes.
Research Project: Steganalysis
In collaboration with the German Federal Office for Information Security (BSI) and the Max-Planck-Institute for Biological Cybernetics at Tübingen, we investigate whether new image models can be used to detect hidden messages in images. As a first step, we compare several image models and use a developed machine learning technique for statistical analysis.
Based on this study, results were presented at several international conferences. Furthermore, a short media contribution was broadcast on SWR 4 and Deutschlandradio and SWR Baden-Württemberg (TV).
This project (together with our industry partner Medav GmbH, Ilmenau, and Prof. Dr. A. Schilling from the University of Tübingen) is supported by a BMBF grant.
The goal of this project is the development of new and more powerful steganalysis methods for images, especially tools for the so-called universal steganalysis, i.e., steganalysis without knowing the specific method of steganographic manipulation. Universal steganalysis requires the statistical characterisation of unmanipulated images. In our case, we will build on our previous experience in image modeling (e.g., our kernel PCA or Wiener series image model) to describe the typical properties of unmanipulated images. A significant deviation from these properties in an image could be used to detect a steganographic manipulation.
Implicit Wiener Series for Higher-Order Image Analysis.
The computation of classical higher-order statistics such as higher-order moments or spectra is difficult for images due to the huge number of terms to be estimated and interpreted. We propose an alternative approach in which multiplicative pixel interactions are described by a series of Wiener functionals. Since the functionals are estimated implicitly via polynomial kernels, the combinatorial explosion associated with the classical higher-order statistics is avoided.
Volterra and Wiener series
In system identification, one tries to infer the functional relationship between system input and output from observations of the in- and outgoing signals. If the system is linear, it can be characterized uniquely by measuring its impulse response, for instance by reverse correlation. For nonlinear systems, however, there exists a whole variety of system representations. One of them, the Wiener expansion, has found a somewhat wider use in neuroscience since its estimation constitutes a natural extension of linear system identification. The coefficients of the Wiener expansion can be estimated by a cross-correlation procedure that is conveniently applicable to experimental data.
Unfortunately, the estimation of the Wiener expansion by cross-correlation suffers from severe problems:
- In practice, the cross-correlations have to be estimated at a finite resolution. The number of expansion coefficients increases with mn for an m-dimensional input signal and an nth-order Wiener kernel such that the resulting numbers are huge for higher-order Wiener kernels. For instance, a 5th-order Wiener kernel operating on 16 x 16 sized image patches contains roughly 1012 coefficients, 1010 of which would have to be measured individually by cross-correlation. As a consequence, this procedure is not feasible for higher-dimensional input signals.
- The estimation of cross-correlations requires large sample sizes. Typically, one needs several tens of thousands of input-output pairs before a sufficient convergence is reached.
- The estimation via cross-correlation works only if the input is Gaussian noise with zero mean, not for general types of input.
- The crosscorrelation method assumes noise-free signals. For real, noise-contaminated data, the estimated Wiener series models both signal and noise of the training data which typically results in reduced prediction performance on independent test sets.
A brief tutorial on Volterra and Wiener series can be found in
[1] Franz, M.O. and B. Schölkopf: Implicit Wiener Series. MPI Technical Report (114), Max Planck Institute for Biological Cybernetics, Tübingen, Germany (June 2003) [PDF].
Implicit estimation via polynomial kernels
We propose a new estimation method based on regression in a reproducing kernel Hilbert space (RKHS) to overcome these problems. Instead of estimating each expansion coefficient individually by cross-correlation, we treat the Wiener series as a linear operator in the RKHS formed by the monomials of the input. The Wiener expansion can be found by computing the linear operator in the RKHS that minimizes the mean square error. Since the basis functions of the Wiener expansion (i.e. the monomials of the components of the input vector) constitute a RKHS, one can represent the Wiener series implicitly as a linear combination of scalar products in the RKHS. It can be shown that the orthogonality properties of the Wiener operators are preserved by the estimation procedure.
In contrast to the classical cross-correlation method, the implicit representation of the Wiener series allows for the identification of systems with high-dimensional input up to high orders of nonlinearity. As an example, we have computed a nonlinear receptive field of a 5th-order system acting on 16 x 16 image patches. The system first convolves the input with the filter mask shown below to the right and feeds the result in a fifth-order nonlinearity. In the classical cross-correlation procedure, the system identification would require the computation of roughly 9.5 billion independent terms for the fifth-order Wiener kernel, and several tens of thousands of data points. Using the new estimation method, the structure of the nonlinear receptive field becomes already recognizable after 2500 data points.
The implicit estimation method is described in
[2] Franz, M. O. and B. Schölkopf: A unifying view of Wiener and Volterra theory and polynomial kernel regression. Neural Computation 18(12), 3097-3118 [PDF].
[3] Franz, M.O. and B. Schölkopf: Implicit estimation of Wiener series. Machine Learning for Signal Processing XIV, Proc. 2004 IEEE Signal Processing Society Workshop, 735-744. (Eds.) Barros, A., J. Principe, J. Larsen, T. Adali and S. Douglas, IEEE, New York (2004) [PDF].
Higher-order statistics of natural images The implicit estimation of Wiener operators via polynomial kernels opens up new possibilities for the estimation of higher-order image statistics. Compared to the classical methods such as higher-order spectra, moments or cumulants, our approach avoids the combinatorial explosion caused by the exponential increase of the number of terms to be estimated and interpreted. When put into a predictive framework, multiplicative pixel interactions of different orders are easily visualized and conform to the intuitive notions about image structures such as edges, lines, crossings or corners. Arbitrarily oriented lines and edges, for instance, cannot be described by the usual pairwise statistics such as the power spectrum or the autocorrelation function: From knowing the intensity of one point on a line alone, we cannot predict its neighbouring intensities. This would require knowledge of a second point on the line, i.e., we have to consider some third-order statistics which describe the interactions between triplets of points. Analogously, the prediction of a corner neighbourhood needs at least fourth-order statistics, and so on.
This can be seen in the following experiment, where we decomposed various toy images into their components of different order.

The behaviour of the models conforms to our intuition: the linear model cannot capture the line structure of the image thus leading to a large reconstruction error which drops to nearly zero when a second-order model is used. Note that the third-order component is only
significant at crossings, corners and line endings.
Pixel interactions up to the order of five play an important role in natural images. Here is an example decomposition:

Reference:
[4] Franz, M.O. and B. Schölkopf: Implicit Wiener series for higher-order image analysis. Advances in Neural Information Processing Systems 17, 465-472. (Eds.) Saul, L.K., Y. Weiss and L. Bottou, MIT Press, Cambridge, MA, USA (2005) [PDF].
Robust estimation with polynomial kernels
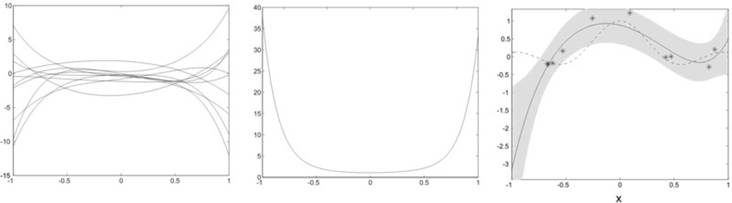
The use of a non-orthonormal function dictionary such as polynomials in ridge regression leads to a non-isotropic prior in function space. This can be seen in a simple toy example where the function to be regressed is a sinc function with uniformly distributed input and additive Gaussian noise. Our function dictionary consists of the first six canonical which are neither orthogonal nor normalized with respect to the uniform input. The effects on the type of functions that can be generated by this choice of dictionary can be seen in a simple experiment: we assume random weights distributed according to an isotropic Gaussian. In our first experiment, we draw samples from this distribution and compute the mean square of the for 1000 functions generated by the dictionary. It is immediately evident that, given a uniform input, our prior narrowly constrains the possible solutions around the origin while admitting a broad variety near the interval boundaries. If we do ridge regression with this dictionary (here we used a Gaussian Process regression scheme), the solutions tend to have a similar behaviour as long as they are not enough constrained by the data points (see the diverging solution at the left interval boundary). This can lead to bad predictions in sparsely populated areas.
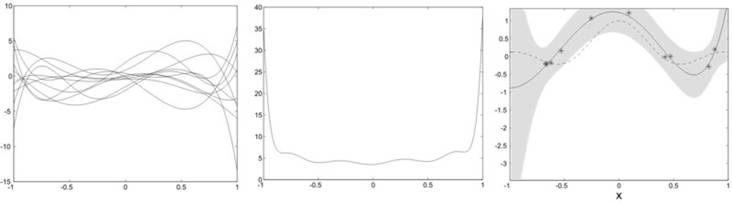
We currently investigate alternative regularization techniques that result in an implicit whitening of the basis functions by penalizing directions in function space with a large prior variance. The regularization term can be computed from unlabelled input data that characterizes the input distribution. Here, we observe a different behaviour: the functions sampled from the prior show a richer structure with a relatively flat mean square value over the input interval. As a consequence, the ridge regression solution usually does not diverge as easily in sparsely populated regions near the interval boundaries.
Reference:
[5] Franz, M.O., Y. Kwon, C. E. Rasmussen and B. Schölkopf: Semi-supervised kernel regression using whitened function classes. Pattern Recognition, Proceedings of the 26th DAGM Symposium LNCS 3175, 18-26. (Eds.) Rasmussen, C. E., H. H. Bülthoff, M. A. Giese and B. Schölkopf, Springer, Berlin, Germany (2004) [PDF]
Learning Interest Operators
 Interest operators find "interesting" locations in images. Existing algorithms are based on heuristic measures, such as local contrast, second order structure, or entropy. Here, we learn an interest operator from human eye movements. This is both benefical in computer vision applications, and it provides insight into the human eye movement system.
Interest operators find "interesting" locations in images. Existing algorithms are based on heuristic measures, such as local contrast, second order structure, or entropy. Here, we learn an interest operator from human eye movements. This is both benefical in computer vision applications, and it provides insight into the human eye movement system.
Iterative Kernel PCA for image modeling
 In contrast to other patch-based modeling approaches such as PCA, ICA or sparse coding, KPCA is capable of capturing nonlinear interactions of the basis elements of the image. The original form of KPCA, however, can be only applied to strongly restricted image classes due to the limited number of training examples that can be processed. We therefore propose a new iterative method for performing KPCA, the Kernel Hebbian Algorithm.
In contrast to other patch-based modeling approaches such as PCA, ICA or sparse coding, KPCA is capable of capturing nonlinear interactions of the basis elements of the image. The original form of KPCA, however, can be only applied to strongly restricted image classes due to the limited number of training examples that can be processed. We therefore propose a new iterative method for performing KPCA, the Kernel Hebbian Algorithm.
Kernel Principal Component Analysis
We investigate the analysis of images based on kernel PCA (KPCA). Memory and time complexity are, however, major obstacles for applying KPCA to huge image databases. The generalized Hebbian algorithm (GHA) provides an efficient implementation of linear PCA with smaller demands on memory complexity. Accordingly, we study the transfer of this property to KPCA by kernelizing the GHA.
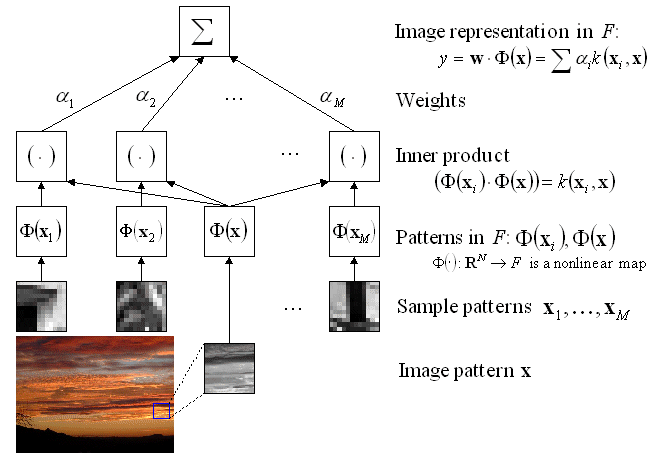
The basic idea of KPCA for image analysis is to nonlinearly map the data into a Reproducing Kernel Hilbert Space (RKHS) F and then perform linear PCA in F. The architecture of KPCA for the extraction of the first principal component is depicted in Fig. 1. A patch of a natural image is fed into the KPCA analyzer. A nonlinear map 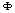 is then applied to map the input into the RKHS F, where the inner product with the principal axis w is computed. These two operations are in practice performed in one single step using the kernel function
is then applied to map the input into the RKHS F, where the inner product with the principal axis w is computed. These two operations are in practice performed in one single step using the kernel function 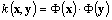 . By expanding the solution w as a linear combination of mapped samples, KPCA indirectly performs PCA in F only based on the kernel function.
. By expanding the solution w as a linear combination of mapped samples, KPCA indirectly performs PCA in F only based on the kernel function.
Kernel Hebbian Algorithm
In the original KPCA formulation, the combination coefficients are computed by diagonalizing the Gram matrix 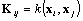 for all sample patterns, which is prohibitive for natural images due to memory complexity. As a nonlinear extension of the Hebbian algorithm, the Kernel Hebbian Algorithm (KHA) estimates them iteratively based on the correlation between the mapped patterns
for all sample patterns, which is prohibitive for natural images due to memory complexity. As a nonlinear extension of the Hebbian algorithm, the Kernel Hebbian Algorithm (KHA) estimates them iteratively based on the correlation between the mapped patterns 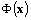 and the system output y in F, which can be efficiently computed based on kernels. This relieves the burden of working directly in a possibly very high-dimensional RKHSs and storing the whole gram matrix.
and the system output y in F, which can be efficiently computed based on kernels. This relieves the burden of working directly in a possibly very high-dimensional RKHSs and storing the whole gram matrix.
Single-frame superresolution
Figs. 3 and 4 show applications of the KHA to image super-resolution. The problem is to reconstruct a high-resolution image based on a low-resolution image. It requires prior knowledge which in our case will be provided by the kernel principal components of a representative dataset of high-resolution image patches. To reconstruct a super-resolution image from a low-resolution image which was not contained in the training set, we first scale up the image to the same size as the training images, then map the image into the F, and project it into the KPCA subspace corresponding to a limited number of principal components. This reconstruction in F is projected back into the input space by preimage techniques.





Image denoising
Fig. 5 shows applications of the KHA to image denoising. No clean training images are required. Instead, it is assumed that the noise mainly contaminates the kernel principal components (KPCs) with small eigenvalues. Thus, a truncated KPC expansion of the noisy image leads automatically to a denoising effect. The KHA is trained and tested on the same data set.





Rank-Deficient Faces
 Finding objects in images is computationally expensive. Here, we learn separable filters that perform object detection tasks. The effectiveness of our approach is illustrated with our face detection library fdlib.
Finding objects in images is computationally expensive. Here, we learn separable filters that perform object detection tasks. The effectiveness of our approach is illustrated with our face detection library fdlib.
Bio-inspired egomotion estimation from optic flow fields
 Tangential neurons in the fly brain are sensitive to the typical optic flow patterns generated during self-motion. We examine whether a simplified model of these neurons can be used to predict the measured motion sensitivities in the fly. The model is tested in a robotic self-motion estimation task.
Tangential neurons in the fly brain are sensitive to the typical optic flow patterns generated during self-motion. We examine whether a simplified model of these neurons can be used to predict the measured motion sensitivities in the fly. The model is tested in a robotic self-motion estimation task.
Computational Modeling of Fly Tangential Neurons
The tangential neurons in the fly brain are sensitive to the typical optic flow patterns generated during self-motion. This suggests a possible involvement in the self-motion estimation process. We compared the measured local preferred directions and motion sensitivities of the VS-neurons (Krapp et al., 1998) to a matched filter model that is optimized for the task of self-motion estimation. In contrast to previous approaches, prior knowledge about distance and self-motion statistics is incorporated in the form of a "world model". We could show that a special case of the matched filter model is able to predict the local motion sensitivities observed in some VS-neurons. This suggests that their receptive field organization can be understood as an adaptation to the processing requirements of estimating self-motion from the optic flow.
In a second study, we examined whether the matched filter model can be used to estimate self-motion from the optic flow. Tests on a mobile robot (modified Khepera) demonstrated that the matched filter approach works for real time camera input and the noisy motion fields computed by Reichardt motion detectors. The achievable accuracy of the proposed approach was investigated in collaboration with the group of Prof. M.V. Srinivasan at the Center of Visual Sciences at the Australian National University in Canberra. We used a gantry carrying an omnidirectional vision sensor that can be moved along three translational and one rotational degree of freedom. The experiments indicate that the proposed approach yields accurate results for rotation estimates, independently of the current translation and scene layout. Translation estimates, however, turned out to be sensitive to simultaneous rotation and to the particular distance distribution of the scene. The gantry experiments confirm that the receptive field organization of the tangential neurons allows them, as an ensemble, to extract self-motion from the optic flow.
